En las entradas anteriores (I, II y III) hemos visto la perplejidad que causó en los hombres de ciencia el descubrimiento y el misterio de los números irracionales.
Para terminar esta exposición queremos preguntarnos qué sabemos a día de hoy sobre estos números. ¿Aumentan los decimales al azar, sin seguir ningún orden determinado? O por el contrario, ¿siguen alguna lógica interna que nos permita conocer el siguiente decimal?
La pregunta ¿tienen fin los números irracionales? no tiene sentido porque si llegáramos aun último decimal, el número ya no sería irracional, sino racional, aunque su número de decimales fuera muy largo.
Pues bien, hay algunos números irracionales en los que estamos empezando a comprender su lógica interna. Veamos algunos ejemplos.
El número pi
El número pi se puede expresar como una función continua. De hecho, esta función puede adoptar diversas formas como se ve en la figura siguiente.
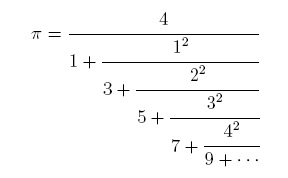
Si observamos esta primera función, veremos que la fracción que permite calcular el número pi es una secuencia de números que sigue hasta el infinito, pero que sigue una cierta regularidad.
En concreto, en el lado derecho de cada denominador nos iremos encontrando una secuencia de números impares (1, 3, 7, 9, etc.) hasta el infinito. Y en cada numerador nos encontraremos una secuencia de números naruales (1, 2, 3, 4, etc.) elevados al cuadrado, hasta llegar al infinito.
Sin embargo, el número pi también admite otro tipo de representación mediante una fracción continua, en concreto, Lange (1999) publicó hace unos años otra manera de representar a este número mediante una fracción.
En este caso, la progresión solo se produce en el numerador de cada fracción. Aquí tenemos los números primos elevados al cuadrado, mientras que a la derecha de la fórmula siempre encontramos el número 6 excepto en el primer caso.
Por lo tanto, en ambos casos hemos encontrado expresiones que nos permiten entrever cierta lógica, dentro de lo ilógico («irracional») que resulta que la mayoría de los números no tengan fin.
El número e
Otro número que ha despertado la curiosidad de numerosos científicos a lo largo de la historia es el número e (2,718281828459045235360…) que se usa como basa para el cálculo de los logaritmos neperianos (ln).
La fracción continua que permite el cálculo de este número es la siguiente.
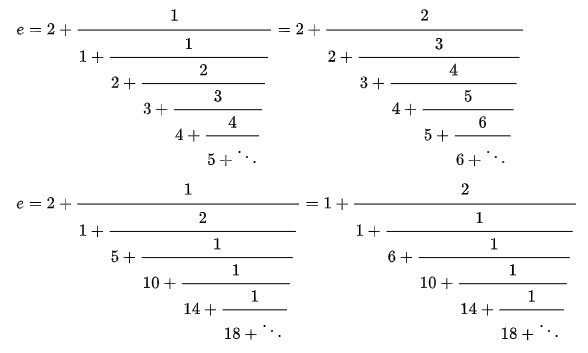
Volvemos a comprobar cómo este número admite diferentes representaciones mediante fracciones continuas.
Números irracionales que se incluyen a sí mismos dentro de la fracción continua
Yendo incluso más allá, nos podemos encontrar con números irracionales que incluyen dentro de la misma fracción el número irracional que pretendemos calcular.
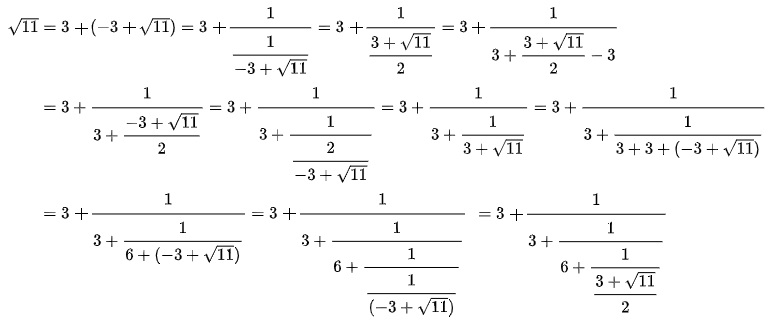
Algunos ejemplos son la raíz cuadrada de 7 y la raíz cuadrada de 11.
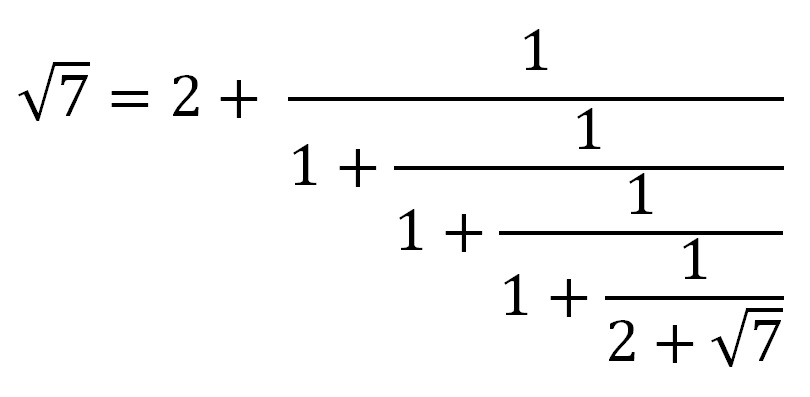
Como se puede comprobar en la fórmula anterior, la fracción no se prolonga hasta el infinito, pero los decimales que se obtienen sí, porque los términos de la fórmula se van insertando una y otra vez en el denominador.
En este caso, vemos cómo además de tratarse de fórmulas finitas pero con decimales infinitos, podemos representar este número irracional mediante diferentes fracciones.
Conclusión
Estos avances nos permiten ir dando pequeños pasos en la comprensión de, en palabras de Newton «saber cómo es el pensamiento de Dios», o en un lenguaje más científico, cuál es la lógica que subyace en algunos números irracionales.
Nos queda todavía mucho por saber sobre la inmensa mayoría de estos números. Por eso, en cierta medida, siguen siendo un misterio. Pero a lo largo de 25 siglos hemos ido dando pequeños pasos para comprender estos números un poco mejor.

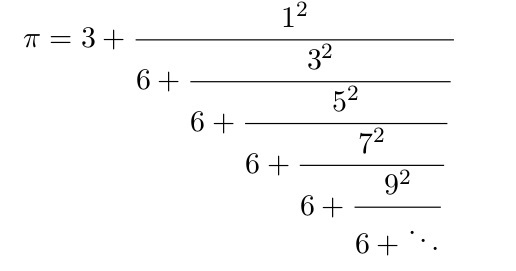







What’s up everyone, it’s my first go to see at this site, and paragraph is truly fruitful in support of me, keep up posting these articles or reviews.