Teorías que explican el condicionamiento clásico

En esta entrada veremos algunas teorías que explican el condicionamiento clásico. No hay ninguna teoría plenamente satisfactoria hasta el momento pero, como veremos, con el paso del tiempo, los diferentes modelos propuestos son capaces de explicar más aspectos de este tipo de aprendizaje asociativo.

Primeros trabajos

Al mismo tiempo en que Pavlov (1927) estudiaba el condicionamiento clásico en Rusia, algunos investigadores trataban de conocer las leyes que rigen el aprendizaje.

Thorndike (1911) fundó la teoría del aprendizaje al empezar a realizar, incluso antes que Pavlov, experimentos de manera sistemática y recoger datos cuantitativos. Propuso que los animales aprenden por ensayo y error. También observó que había limitaciones biológicas en el aprendizaje (los animales de distintas especies tenían diferentes capacidades para aprender las respuestas).

Este autor propuso tres leyes para explicar el aprendizaje:

• Ley del efecto: aquellas respuestas que van seguidas de bienestar, tienen más probabilidad de volver a ocurrir. Por el contrario, las respuestas que van seguidas de malestar, tienen menor probabilidad de ocurrir en el futuro. El aprendizaje consistiría en conexiones E-R (estímulo respuesta), en lugar de meras asociaciones de ideas, como sugerían los empiristas británicos.
• Ley del ejercicio: una vez que se ha creado una conexión E-R, la fuerza de la conexión se refuerza cada vez que se vuelve a realizar la respuesta. Es decir, la repetición de la respuesta no sirve para aprender (establecer una conexión E-R nueva), sino para hacer más fuerte una conexión E-R ya existente, que había sido creado siguiendo la ley del efecto.
• Ley de la disposición: hay ciertas conexiones E-R que se producen con mayor facilidad que otras, por el hecho de estar predeterminadas biológicamente (por ejemplo, los cerdos aprenderán más rápidamente a escarbar con el hocico para encontrar comida, mientras que las palomas aprenderán a picotear una palanca con mayor facilidad, etc.).

Hull y la variable del organismo

Unos años más tarde, Hull (1943) propuso una teoría del aprendizaje en la que defendía que el aprendizaje permite a los organismos adaptarse al medio. Para él, en el aprendizaje se debía aplicar el paradigma: estímulo → variables fisiológicas del organismo → respuesta (E→O→R).

Este autor consideraba que los diferentes estímulos sensoriales (E) afectaban al organismo (O), y como consecuencia de esta afectación, se acababa emitiendo una respuesta (R). Además, que esta respuesta fuera más o menos intensa dependería de las características del estímulo (por ejemplo, de su intensidad) y también de los “estados hipotéticos del organismo” o “variables intervinientes”.

En el modelo de Hull, el reforzamiento es el factor principal que determina el aprendizaje. Este reforzamiento consigue reducir el impulso del organismo. Por ejemplo, consideremos una paloma que tiene sed y presionando una palanca obtiene agua. El reforzador (agua) conseguirá reducir el impulso interno de beber y, por lo tanto, tras varias presiones de la palanca dejará de realizar esta conducta.

Para Hull, el reforzamiento solamente ocurre si cubre una necesidad. Los animales mantendrán sus conductas mientras sean eficaces para reducir el impulso.

Por último, lo que el animal aprende se va convirtiendo en hábito, y de esta manera, podemos calcular la fuerza del hábito como cantidad total del aprendizaje adquirido.

Kamin y la sorpresa del EI

Por otro lado, Kamin (1969) descubrió la existencia del bloqueo y ello le llevó a proponer que el aprendizaje dependía del grado de sorpresa que el estímulo incondicionado provocara sobre el organismo. Más tarde se comprobó que este modelo también era capaz de explicar el ensombrecimiento, que ya había sido descrito por Pavlov años antes.

A partir de estos trabajos, algunos autores trataron de desarrollar un modelo matemático que explicara los resultados encontrados tanto en el procedimiento estándar, como en los fenómenos especiales de condicionamiento clásico.

Modelo de Rescorla y Wagner (1972)

Rescorla y Wagner (1972) propusieron un modelo de aprendizaje por condicionamiento clásico en el que la fuerza de la asociación entre el EC y el EI se desarrolla a lo largo de los diferentes ensayos. Cada vez que ambos estímulos se presentan de manera conjunta, se está proporcionando información sobre la contingencia que guardan entre ellos.

Para estos autores, cuando un estímulo forma parte de un compuesto (en el que hay otros estímulos, por ejemplo: EC1 y EC2), la fuerza asociativa total que conseguirá cada estímulo dependerá de la fuerza asociativa total del compuesto. Es decir, no solamente de la fuerza asociativa de cada uno de sus componentes por separado.

En otras palabras, la cantidad de aprendizaje conseguida por un EC en un ensayo determinado dependerá de la fuerza asociativa conseguida por todos los estímulos presentados en ese ensayo y en los anteriores.

En cada ensayo, el cambio que se conseguirá en la fuerza asociativa (∆V_A) del estímulo condicionado A (EC_A) será:

∆V_Aⁿ = α_A β (λ – ΣV ^n-1)

Donde:

– n es el número de ensayo en el que nos encontramos dentro del experimento

– α es un parámetro que nos indica la saliencia (intensidad o prominencia) del estímulo que queremos condicionar. Este modelo parte del supuesto de que diferentes estímulos neutros se podrán condicionar a diferentes velocidades, aunque ambos reciban el mismo refuerzo. Este valor siempre estará contenido dentro del intervalo 0 ≤ α ≤1. Un valor de α bajo próximo a 0 indicará que es un estímulo neutro difícil de condicionar y que, por lo tanto, su aprendizaje será lento, mientras que un EC con un alfa elevado o próximo a 1 indicará que el aprendizaje se realizará con rapidez.

– β nos indica la rapidez o facilidad con la que el estímulo incondicionado se podrá asociar a los estímulos neutros presentes en el condicionamiento. Al igual que α, su valor podrá variar entre 0 y 1 (0 ≤ β ≤1). Un valor próximo a 0 indicará que se trata de un EI lento o difícil de condicionar, y un valor elevado o próximo a 1 indicará que se trata de un EI fácil de condicionar.

– λ es el nivel asintótico de la fuerza asociativa que un EI puede provocar. Es decir, el nivel máximo de aprendizaje que será posible conseguir.

–  ΣV ^n-1 es la suma de todas las fuerzas asociativas conseguidas por todos los EC presentes en el experimento hasta el ensayo anterior. Es decir, si estamos en el ensayo 5, ΣV ^n-1 sería la suma de todas las fuerzas asociativas conseguidas por los estímulos condicionados presentes (EC1, EC2, etc.) hasta el ensayo 4.

Por otro lado, podemos saber la fuerza asociativa total conseguida en un ensayo n por parte de un estímulo condicionado A (V_Aⁿ) mediante la siguiente fórmula:

V_Aⁿ = V_A^n-1 + ∆V_Aⁿ

Donde:

– V_A^n-1 es la fuerza asociativa conseguida por el EC_A hasta el ensayo anterior

– ∆V_Aⁿ es el incremento de fuerza asociativa en el ensayo n

Ejemplo de aplicación del Modelo de Rescorla y Wagner (1972)

Veamos un ejemplo de aplicación práctica de este modelo:

Sea un procedimiento de condicionamiento clásico estándar formado por un tono (EC_T) y una descarga eléctrica (EI). ¿Cuál es la fuerza asociativa conseguida por el tono en el ensayo 5?

Datos: El tono tiene una saliencia de 0,9, la descarga eléctrica de 0,8, y la cantidad máxima de aprendizaje es de 1.

Los valores que vamos a utilizar para realizar los cálculos serán:

α = 0,9; β = 0,8; λ = 1

En el ensayo 1, el incremento de fuerza asociativa del tono (∆V_T¹) será:

∆V_T¹ = 0,9 * 0,8 * (1 – 0) = 0,72

Por lo tanto, la fuerza asociativa total conseguida por el tono en el ensayo 1 será:

V_T¹  = 0 + 0,72 = 0,72

En el ensayo 2, el ∆V_T² será:

∆V_T² = 0,9 * 0,8 * (1 – 0,72) = 0,2016

Y la fuerza asociativa conseguida será:

V_T²  = 0,72 + 0,2016 = 0,9216

En el ensayo 3, el ∆V_T³ será:

∆V_T³ = 0,9 * 0,8 * (1 – 0,9216) = 0,0565

Y la fuerza asociativa:

V_T³  = 0,9216 + 0,0565 = 0,9781

En el ensayo 4, el ∆V_T4 será:

∆V_T⁴ = 0,9 * 0,8 * (1 – 0,9781) = 0,0158

Y la fuerza asociativa:

V_T⁴  = 0,9781 + 0,0158 = 0,9939

Por último, en el ensayo 5, el ∆V_T⁵ será:

∆V_T⁵ = 0,9 * 0,8 * (1 – 0,9939) = 0,0044

Y la fuerza asociativa total (V_T⁵):

V_T⁵  = 0,9939 + 0,0044 = 0,9983

Por lo tanto, la fuerza asociativa conseguida en el ensayo 5 es de 0,9983. Es un valor muy próximo a 1, lo que indica que, en los 5 primeros ensayos, el estímulo condicionado (es decir, el tono) ha conseguido casi toda la fuerza asociativa disponible para este condicionamiento. Podemos representar los datos en una gráfica para observar mejor cómo se ha conseguido esta adquisición.

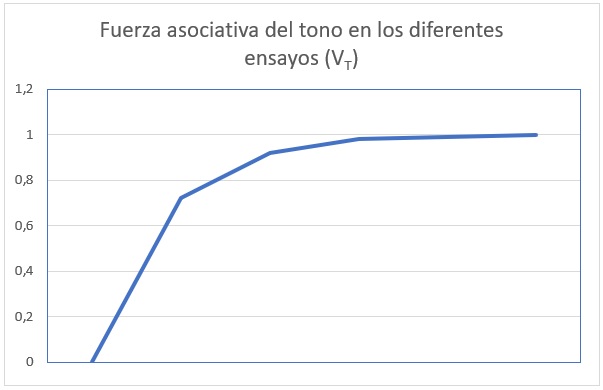
Como se puede comprobar, se ha producido un proceso normal de adquisición, con un incremento rápido en la fuerza asociativa en los primeros ensayos, y con una desaceleración, hasta llegar a un valor asintótico, próximo a 1, en los siguientes.

Aplicaciones y limitaciones del Modelo de Rescorla y Wagner (1972)

El modelo de Recorla y Wagner (1972) permite explicar de manera adecuada el proceso de adquisición, pero no el de extinción ni el de recuperación espontánea. No hay nada, en este modelo que nos diga porqué, si el EC se sigue presentando sin estar emparejado con el EI, éste irá perdiendo de manera progresiva su fuerza asociativa (extinción). Ni porqué, una vez perdida ésta, con el mero paso del tiempo, la fuerza asociativa puede volver a aparecer.

Sin embargo, dicho modelo puede explicar de manera adecuada por qué se produce el bloqueo y el ensombrecimiento. En el apartado de ejercicios de este tema se presentan algunos ejemplos. Aquí solamente explicaremos cómo se deberían realizar los cálculos si tuviéramos más de un EC.

Si tenemos un EC_A y un EC_X, los incrementos de sus respectivas fuerzas asociativas serían:

∆V_Aⁿ = α_A β (λ – ΣV ^n-1)

y

∆V_Xⁿ = α_X β (λ – ΣV ^n-1)

Mientras que el cálculo de las fuerzas asociativas totales conseguidas en un ensayo determinado serían:

V_Aⁿ = V_A^n-1 + ∆V_Aⁿ

y

V_Xⁿ = V_X^n-1 + ∆V_Xⁿ

Modelo de Mackintosh (1975)

Unos años más tarde, Mackintosh (1975) propuso una explicación alternativa para el condicionamiento clásico. Según este autor, el aprendizaje se explicaría por la existencia de variaciones en el nivel atención (en lugar de por la competición entre estímulos por una fuerza asociativa limitada, como habían propuesto Rescorla y Wagner en 1972).

Mackintosh consideraba que la atención es un recurso limitado, de manera que, un estímulo que es significativo, es decir, que aporta información relevante, puede atraer la atención, y de esta manera, limitar la capacidad de aprendizaje de otros estímulos (Shanks, 2009).  

La reducción en la capacidad para adquirir fuerza asociativa se debe a los cambios en la atención prestada al EC. Lo que provoca que los EC sean, en ocasiones, bloqueados o ensombrecidos, y por lo tanto, que resulten más difíciles de condicionar, es una disminución de la atención que se presta a dichos estímulos (Vidal, 2015).

La competición entre estímulos no sucede porque el refuerzo deje de ser efectivo, sino porque los animales ignoran unos estímulos condicionados en presencia de otros estímulos condicionados que predicen en mayor grado la aparición del estímulo incondicionado (Vidal, 2015).

El modelo Mackintosh tiene una ventaja respecto al de Rescorla y Wagner, y es que permite explicar, además del bloqueo y del ensombrecimiento, la inhibición latente la irrelevancia aprendida, tanto en el condicionamiento clásico excitatorio como inhibitorio.

Recordemos que, en la inhibición latente, un EC se presentaba varias veces, en una primera fase, de manera aislada. Según el modelo de Rescorla y Wagner, la saliencia del EI (β) en esta fase sería 0, por lo que el incremento de la fuerza asociativa en estos ensayos (∆V_Aⁿ) también debería ser 0. Por lo tanto, no habría aprendizaje.    

Sin embargo, para Mackintosh, cuando hay varios estímulos condicionados disponibles, la atención prestada a uno de ellos (llamado α, saliencia o asociabilidad) en cada ensayo cambia según la siguiente relación:

∆α_A es positivo si |λ – V_A| < |λ – V_X|

∆α_A es negativo si |λ – V_A| ≥ |λ – V_X|

Donde:

– λ es la fuerza asociativa asintótica que puede ser condicionada por el reforzador

– V_A es la fuerza asociativa actual del estímulo condicionado A

– V_X es la fuerza asociativa de todos los estímulos diferentes a presentes en ese ensayo

De esta manera, la expresión |λ – V_A| indica el nivel en el que el EC_A predice la aparición del EI. Por otro lado, |λ – V_X| se refiere al grado en el que el resto de EC presentes en el condicionamiento predicen la aparición del EI.

En resumen:

– α_A aumentará si el estímulo condicionado A (EC_A) predice la aparición de un estímulo incondicionado que sería inesperado si no apareciera este EC_A.

– α_A disminuirá si el estímulo condicionado A (EC_A) no predice ningún cambio en el estímulo incondicionado.

Aplicaciones y limitaciones del Modelo de Mackintosh (1975)

Por lo tanto, Mackintosh consigue explicar, además del procedimiento general, distintos fenómenos del condicionamiento clásico:

• Procedimiento general de condicionamiento clásico: el individuo presta atención al único EC presente en la situación de condicionamiento. Como V_X será igual a 0, se cumplirá que |λ – V_A| < |λ|, y el ∆α_A será positivo, es decir, EC_A adquirirá fuera asociativa en cada ensayo, porque sujeto le estará prestando atención.
• Bloqueo: en unos ensayos previos, un EC se habrá asociado al EI, como veíamos con Rescorla y Wagner. Cuando llegamos a la fase 2, en la que presentamos el condicionamiento compuesto, con más de un EC, nos encontramos con que el estímulo presentado en la fase 1 ya había adquirido mucha fuerza asociativa. Imaginemos que el estímulo nuevo añadido en la fase 2 se llama EC_A. Nos encontraremos con que |λ – V_A| ≥ |λ – V_X|, porque V_x, es decir, la fuerza asociativa del resto de estímulos, es mayor. Al cumplirse esta relación, α_A (la saliencia del EC_A) tenderá a ser cada vez menor. En otras palabras, el individuo no le prestará atención y, por lo tanto, no se condicionará al EI. Si presentamos en la fase 3 el EC_A de manera aislada, podremos comprobar que no emite la RC. En definitiva, ha sido bloqueado.
• Ensombrecimiento: partimos de un condicionamiento compuesto, en el que un estímulo α_A es menos saliente (intenso o prominente) que otro estímulo (lo llamaremos X). En los primeros ensayos se cumplirá |λ – V_A| ≥ |λ – V_X|, por lo tanto, la α_A será cada vez menor. El α_A habrá sido ensombrecido.
• Inhibición latente: En este caso, si presentamos previamente el EC_A sin ir emparejado de ningún EI, el individuo habrá aprendido a ignorarlo, por lo que α_A se habrá ido haciendo, de manera progresiva, cada vez menor. Cuando se presenten juntos (el EC_A y el EI), el EC_A partirá de una α_A baja. Cualquier otro estímulo que haya en el medio, aunque sea de manera fortuita (el sonido de un ventilador, un cambio en la iluminación de la sala, un olor, etc.) tendrá una fuerza asociativa (V_x) mayor. Por lo tanto, |λ – V_A| ≥ |λ – V_X|, es decir, la saliencia del EC_A se irá haciendo cada vez más pequeña, y el estímulo habrá tenido una inhibición latente.
• Irrelevancia aprendida:algo similar ocurre en este caso. El individuo ha aprendido el EC_A no se empareja siguiendo una relación de contingencia con el EI. Por lo tanto, su α_A se habrá ido haciendo cada vez menor. Cuando otro estímulo presente en el medio, tendrá una V_x mayor. Es decir, |λ – V_A| ≥ |λ – V_X|, lo que hará que α_A sea cada vez menor, porque al EC_A se le presta cada vez menor atención.

Condicionamiento excitatorio e inhibitorio: los sujetos deberán prestar igualmente atención a los estímulos que indican la aparición del EI como a los estímulos que indican su no aparición. Por lo tanto, este modelo sirve también para explicar el condicionamiento clásico inhibitorio.

Modelo de Pearce y Hall (1980)

Por último, Pearce y Hall (1980) propuso un modelo totalmente opuesto a los anteriores. Para estos autores, la atención decrece en los estímulos que tienen un valor predictivo estable. Es decir, el individuo atenderá a aquellos estímulos que sean seguidos de consecuencias imprevistas por este sujeto. Dichos estímulos imprevistos tendrán mayores probabilidades de ser tenidos en cuenta por el sistema de procesamiento del sujeto y, por lo tanto, de ser condicionados.

De esta manera, si un EC está totalmente emparejado con un EI irá perdiendo la atención del sujeto.

Esta idea se expresa mediante la fórmula:

α_Aⁿ = |λ^n-1 – V_A^n-1|

Donde:

– α_Aⁿ es el nivel de asociabilidad del estímulo condicionado A en el ensayo n. Depende del valor absoluto de la discrepancia entre la intensidad del EI (λ) en el ensayo previo (n-1) y de la fuerza asociativa

– λ^n-1 es la magnitud del estímulo incondicionado presentado en el ensayo n-1

–  V_A^n-1 es la magnitud esperada del estímulo incondicionado, según el conocimiento previo del individuo

Por lo tanto, en el ensayo n-1 espera que el EI se presente de una manera determinada (siguiendo una frecuencia, intensidad, duración, etc.). Si sucede lo que esperaba, es decir, si la discrepancia |λ^n-1 – V_A^n-1| es pequeña, la atención prestada al EC_A se hará más pequeña.

Por el contrario, si hay grandes cambios entre lo que se esperaba que iba a pasar y lo que realmente sucede, la discrepancia |λ^n-1 – V_A^n-1| se hará mayor, y la atención hacia el EC_A crecerá.

Cuando el sujeto se pregunte “¿qué es esto?”, “¿por qué se ha producido este cambio?” empezará a prestar atención a otros estímulos del medio, entre los que estará el EC_A para tratar de determinar qué es lo que ha provocado este cambio.

El modelo de Pearce y Hall (1980) es el que permite explicar un número de fenómenos de condicionamiento clásico mayor, porque tiene en cuenta los cambios en el procesamiento del EC (α), pero también, los cambios en el EI, tanto en su magnitud presentada (λ), como en la esperada (V).

Bibliografía

Hull, C. (1943). The principles of psychology: An introduction to behavior theory. Nueva York: Century Crofts.

Kamin, L. (1969). Predictability, surprise, attention and conditioning. En B. C. Campbell, Punishment and Aversive Control (págs. 279-296). Nueva York: Applenton-Century-Crofts.

Mackintosh, N. (1975). A Theory of Attention: Varitions in the Associability of Stimuli with Reinforcement. Psychological Review, 82(4), 276-298.

Pavlov, I. (1927). Conditioned reflexes. Londres: Oxford University Press.

Pearce, J., & Hall, G. (1980). A Model for Pvlovian Learning: Variations in the Effectiveness of Conditioned but Not of Unconditioned Stimuli. Psychological Review, 532-552.

Rescorla, R., & Wagner, A. (1972). A Theory of Pavlovian Conditioning: Variations in the Effectiveness of Reinforcement and Nonreinforcement. En A. P. Black, Classical Conditioning II: Current Research and Theory (págs. 64-99). Nueva York: Appleton-Century-Crofts.

Shanks, D. (2009). Editor’s Introduction: Psychology of Learning. En D. Shanks, Psychology of Learning (págs. XVII-XXXII). Londres: SAGE Publications Ltd.

Thorndike, W. (1911). Animal intelligence: An experimental study of the associative process in animals. Nueva York: McMillan.

Vidal, J. (2015). Condicionamiento clásico pavloviano. En E. Muñoz, I. Pozo, J. Sansa, & J. Vidal, Psicología del aprendizaje (págs. 1-75). Barcelona: Oberta UOC Publishing, S.L.

Ejercicio 1. (Todas las soluciones se encuentran al final)

Explica el siguiente diseño experimental:

Grupos	Fase 1	Fase 2	Fase de prueba
Experimental	EC	EC – EI	EC
Control		EC -EI	EC

Actividad 1. ¿Cómo se llama el fenómeno especial de aprendizaje que se muestra en este ejercicio?

Actividad 2. Explica este fenómeno desde las perspectivas teóricas del condicionamiento clásico propuestas por Rescorla y Wagner (1972), Mackintosh (1975) y Pearce y Hall (1980). Indica cuáles de ellas permiten explicar de manera satisfactoria los resultados hallados en este tipo de diseño experimental.

 Actividad 3. Los resultados de la fase de prueba se muestran a continuación:

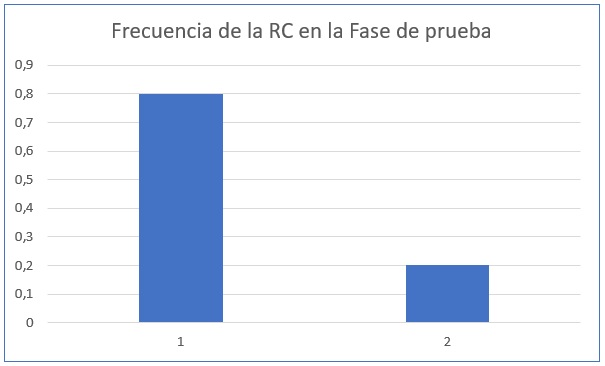
¿A qué grupos, experimental y control, corresponden los números 1 y 2 de la gráfica?

Actividad 4. ¿Qué autores, de los enumerados en el enunciado de la Actividad 2, permiten explicar estos resultados?

Ejercicio 2.

En un laboratorio se presenta a un grupo de ratas la siguiente situación experimental:

Fase 1	Fase de prueba
6 (EC1 – EC2 – EI)	EC1 EC2

Tenemos los siguientes datos: α₁ = 0,2; α₂ = 0,7; β = 0,4; λ = 1.

Actividad 1. ¿Qué tipo de fenómeno especial de condicionamiento clásico crees que se producirá?

Actividad 2. Realiza los cálculos de la fuerza asociativa propuestos por Rescorla y Wagner (1972) e indica si se han cumplido las predicciones realizadas en la actividad anterior.

Actividad 3. ¿Cómo se explicarían estos resultados desde la teoría de Mackintosh (1975)? ¿Y desde la teoría de Pearce y Hall (1980)?

Soluciones

Ejercicio 1 (Solución)

Actividad 1

Se trata de un diseño experimental correspondiente a una inhibición latente. Se realiza una preexposición de un estímulo condicionado. Esta exposición previa dificulta su condicionamiento posterior.

Actividad 2

Rescorla y Wagner (1972) consideraban que en la Fase 1 no se iba a producir ningún tipo de aprendizaje, porque al no presentarse el EI, β = 0. Mientas que en la Fase 2 se debería producir un proceso normal de adquisición del condicionamiento clásico.

Mackintosh (1975) consideraba que en la Fase 1 el sujeto habrá aprendido a ignorar el EC, por lo que cuando se presente en la fase 2, su α_A será pequeña, y cualquier otro estímulo presente en el ambiente tendrá mayor capacidad para condicionarse. Es decir, |λ – V_A| ≥ |λ – V_X|. Así, la saliencia del EC_A se irá haciendo cada vez más pequeña, y el estímulo habrá tenido una inhibición latente.

Por último, Pearce y Hall (1980) consideran que el nivel de atención prestado al EI en la Fase 2 será pequeño. Ello se debe a que, en los ensayos anteriores, el EC se había presentado en solitario y el sujeto había aprendido a ignorarlo. Cuando se presente el EI por primera vez, aunque lo haga asociado al EC, el individuo buscará qué otras cosas han cambiado en el ambiente (un pequeño sonido, una luz, un olor, etc.) que lo hagan buen predictor del EI. Pero como el EC partirá de una α_A muy baja, será difícil que sea procesado y que, por lo tanto, se acabe asociando al EI.

Actividad 3

El número 1 corresponde al grupo de control. Dado que no ha habido una preexposición previa al EC, se ha producido un proceso normal de adquisición.

Por otro lado, el número 2 corresponde al grupo experimental. La preexposición previa impide que el EC se pueda condicionar con normalidad en las fases posteriores del experimento. Por eso se observa una baja frecuencia en la respuesta condicionada.

Actividad 4

Tanto Mackintosh (1975) como Pearce y Hall (1980) permiten explicar esta inhibición latente.

El modelo de Rescorla y Wagner (1972) no puede explicar estos resultados porque predice un nivel de respuesta condicionada ante la presentación del EC similar en ambos grupos.

Ejercicio 2 (Solución)

Actividad 1

Dado que el EC2 es más intenso o prominente que el EC1, es probable que el EC2 quede ensombrecido por el EC1.

Por lo tanto, es probable que se produzca un ensombrecimiento.

Actividad 2

Ensayo 1

Los incrementos de la fuerza asociativa para los EC1 y EC2 serán:

∆V₁¹ = 0,2 * 0,4 * (1 – 0) = 0,0800

∆V₂¹ = 0,7 * 0,4 * (1 – 0) = 0,2800

Las fuerzas asociativas de cada estímulo serán:

V₁¹ = 0 + 0,0800 = 0,0800

V₂¹ = 0 + 0,2800 = 0,2800

Y la fuerza asociativa total en el ensayo 1 será:

V¹ = 0,3600

Ensayo 2

Los incrementos de la fuerza asociativa para los EC1 y EC2 serán:

∆V₁² = 0,2 * 0,4 * (1 – 0,3600) = 0,0512

∆V₂² = 0,7 * 0,4 * (1 – 0,3600) = 0,1792

Las fuerzas asociativas de cada estímulo serán:

V₁² = 0,0800 + 0,0512 = 0,1312

V₂² = 0,2800 + 0,1792 = 0,4592

Y la fuerza asociativa total en el ensayo 1 será:

V² = 0,1312 + 0,4592 = 0,5904

Ensayo 3

Los incrementos de la fuerza asociativa para los EC1 y EC2 serán:

∆V₁³ = 0,2 * 0,4 * (1 – 0,5904) = 0,0328

∆V₂³ = 0,7 * 0,4 * (1 – 0,5904) = 0,1147

Las fuerzas asociativas de cada estímulo serán:

V₁³ = 0,1312+ 0,0328 = 0,1640

V₂³ = 0,4592 + 0,1147 = 0,5739

Y la fuerza asociativa total en el ensayo 3 será:

V³ = 0,1640 + 0,5739 = 0,7379

Ensayo 4

Los incrementos de la fuerza asociativa para los EC1 y EC2 serán:

∆V₁⁴ = 0,2 * 0,4 * (1 – 0,7379) = 0,0210

∆V₂⁴ = 0,7 * 0,4 * (1 – 0,7379) = 0,0734

Las fuerzas asociativas de cada estímulo serán:

V₁⁴ = 0,1640 + 0,0210 = 0,1850

V₂⁴ = 0,5739 + 0,0734 = 0,6473

Y la fuerza asociativa total en el ensayo 3 será:

V⁴ = 0,1850 + 0,6473 = 0,8323

Ensayo 5

Los incrementos de la fuerza asociativa para los EC1 y EC2 serán:

∆V₁⁵ = 0,2 * 0,4 * (1 – 0,8323) = 0,0134

∆V₂⁵ = 0,7 * 0,4 * (1 – 0,8323) = 0,0470

Las fuerzas asociativas de cada estímulo serán:

V₁⁵ = 0,1850 + 0,0134 = 0,1984

V₂⁵ = 0,6473 + 0,0470 = 0,6943

Y la fuerza asociativa total en el ensayo 3 será:

V⁵ = 0,1984 + 0,6943 = 0,8927

Ensayo 6

Los incrementos de la fuerza asociativa para los EC1 y EC2 serán:

∆V₁⁶ = 0,2 * 0,4 * (1 – 0,8927) = 0,0086

∆V₂⁵ = 0,7 * 0,4 * (1 – 0,8927) = 0,0300

Las fuerzas asociativas de cada estímulo serán:

V₁⁵ = 0,1984 + 0,0086 = 0,2070

V₂⁵ = 0,6943 + 0,0300 = 0,7243

Y la fuerza asociativa total en el ensayo 3 será:

V⁵ = 0,2070 + 0,7243 = 0,9313

En efecto, se han cumplido las predicciones, porque el EC1 ha conseguido mucha menos fuerza asociativa (V₁⁵ = 0,2070) que el EC2 (V₂⁵ = 0,7243). Por lo tanto, el EC2 ha ensombrecido el EC1 al tratarse de un estímulo más saliente (intenso o prominente).

Actividad 3

La teoría de Mackintosh (1975) consideraría que el estímulo 1 tendría una α₁ más pequeña que el estímulo 2. Por eso, en los primeros ensayos se cumplirá |λ – V_A| ≥ |λ – V_X|, y esto hará que, en los ensayos sucesivos, el α₁ se iría haciendo cada vez menor. El individuo prestaría cada vez menos atención al EC1 y éste resultaría ensombrecido.

La teoría de Pearce y Hall (1980) considera que los organismos tienen una capacidad de procesamiento limitada. Esto hace el sujeto se centre en prestar atención a los estímulos que no sean buenos predictores de las consecuencias. Cuando se presente el EI y genere sorpresa en el sujeto, éste buscará en el medio los EC que puedan explicar esta aparición. El estímulo más saliente o prominente será el que capte más recursos atencionales (en nuestro caso será el EC2) y el otro estímulo (EC1) resultará ensombrecido.